7 Facts You Must Know About Menelaus’ Theorem

Menelaus' Theorem is a fundamental concept in geometry.

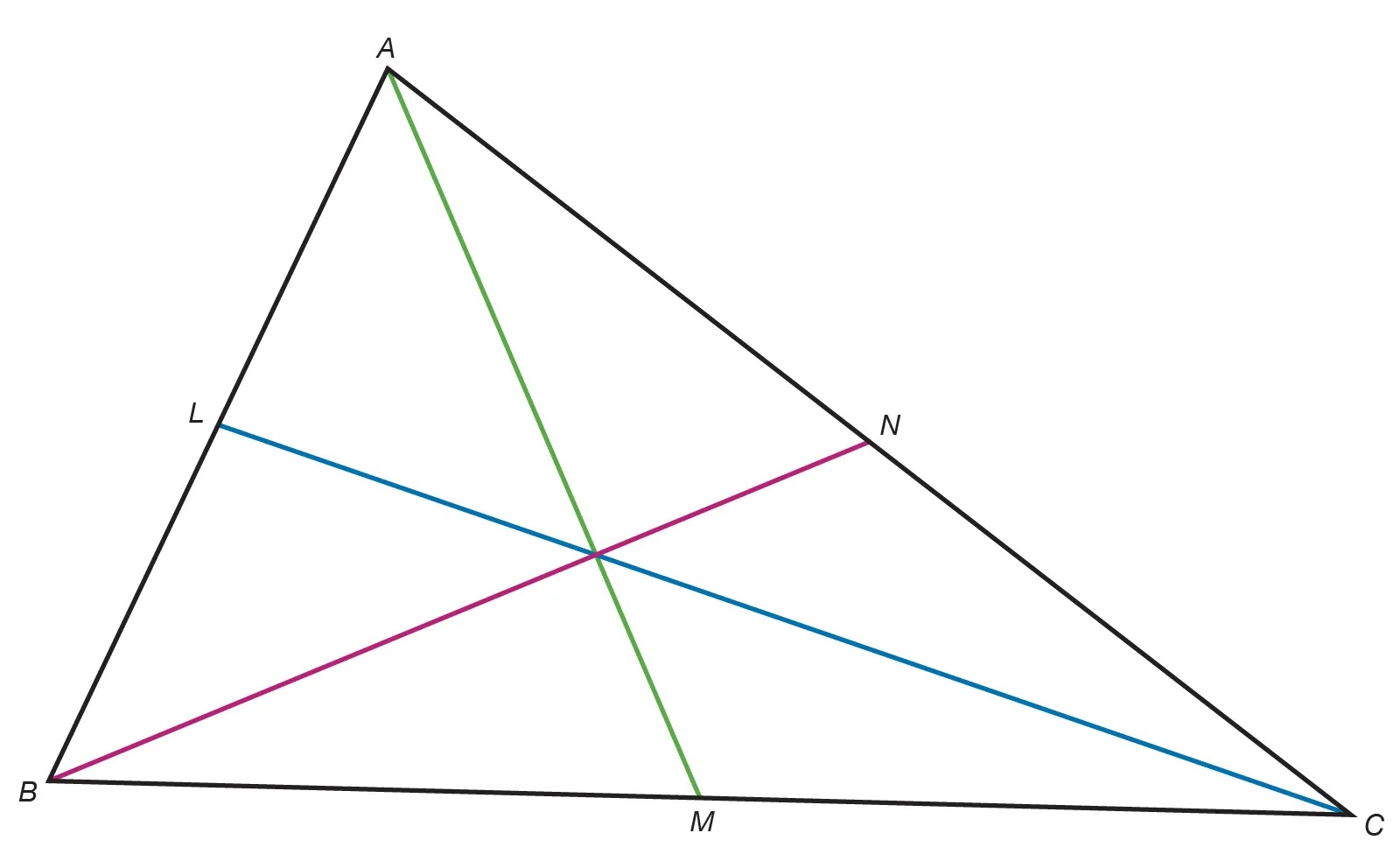
Menelaus' Theorem, named after the ancient Greek mathematician Menelaus of Alexandria, is a crucial theorem in Euclidean geometry. It provides a relationship between the ratios of the lengths of the three cevians of a triangle, which are lines that connect a vertex of a triangle to a point on the opposite side. This theorem has significant applications in various fields, including engineering, architecture, and navigation.

It is used to establish a relationship between the cevians of a triangle.

Menelaus' Theorem is employed to establish a relationship between the cevians of a triangle. By utilizing this theorem, mathematicians and engineers can solve complex geometric problems involving triangles and their cevians. This relationship is instrumental in determining the lengths of cevians and understanding the geometric properties of triangles.

The theorem is based on the concept of collinearity.

At its core, Menelaus' Theorem is based on the concept of collinearity, which refers to points lying on the same straight line. This fundamental geometric principle forms the basis of the theorem's application and is essential for understanding the relationships between the cevians of a triangle.

Menelaus' Theorem is a powerful tool for solving geometric problems.

With its ability to establish relationships between cevians and their lengths within a triangle, Menelaus' Theorem serves as a powerful tool for solving a wide array of geometric problems. Its applications extend to diverse fields, including architecture, surveying, and computer graphics, making it an indispensable concept in the realm of geometry.

It is a key component in projective geometry.

Menelaus' Theorem plays a pivotal role in projective geometry, a branch of mathematics that deals with the properties of geometric figures that are invariant under projection. This theorem's significance in projective geometry underscores its relevance in advanced mathematical concepts and its broader implications in the field of mathematics.

The theorem has historical significance in the development of geometry.

Menelaus' Theorem holds historical significance in the development of geometry, representing a crucial advancement in the understanding of geometric relationships and properties. Its enduring relevance and applications have contributed to its status as a foundational concept in the realm of geometry.

Menelaus' Theorem is an essential component of geometric problem-solving.

In the realm of geometric problem-solving, Menelaus' Theorem stands as an essential component, providing mathematicians, engineers, and scholars with a powerful tool for tackling intricate geometric challenges. Its versatility and applications underscore its enduring importance in the field of mathematics and its practical utility in various real-world scenarios.

Menelaus' Theorem, a cornerstone of Euclidean geometry, continues to exert its influence across diverse domains, serving as a testament to the enduring significance of mathematical principles in shaping our understanding of the world.

Conclusion

In conclusion, Menelaus' Theorem is a powerful tool in the field of geometry, offering a systematic approach to solving complex problems related to triangles and their associated line segments. By understanding the fundamental principles and applications of this theorem, mathematicians and students alike can unlock new perspectives and strategies for tackling geometric challenges. From its historical significance to its practical implications in modern mathematics, Menelaus' Theorem continues to inspire curiosity and exploration in the realm of geometry.

FAQs

What is the historical significance of Menelaus' Theorem?Menelaus' Theorem is named after the ancient Greek mathematician Menelaus of Alexandria, who made significant contributions to geometry. His theorem has stood the test of time and remains a cornerstone of geometric principles.

How is Menelaus' Theorem applied in modern mathematics?Menelaus' Theorem has diverse applications in various fields, including engineering, computer graphics, and navigation. It provides a systematic approach to solving geometric problems involving triangles and their associated line segments.